数列的极限
想看点物理的拓展,然后发现怎么也逃不出微分和积分。。。
好吧那就来看看吧。
数列的极限
极限定义:epsilon-N语言
数列是什么就不多说了,当数列$\{x_{n} \}$的$n \rightarrow \infty $时,它对应的$x_{n}$如果能够无限接近于一个确定的数值,那么就称这个数为数列$\{x_{n}\}$的极限。
那么怎么用数学语言来定义呢,我们先给出定义再解释为什么:
定义:设$\{x_{n} \}$为一数列,如果存在任意常数$a$,对于任意给定的正数$\varepsilon$,不论它有多小,总存在正整数$N$,使得当$n>N$时,不等式
都成立,那么就称常数$a$是数列$\{x_{n}\}$的极限。
记为
这是什么意思呢?
首先要明确的是,a是最终接近的数,$x_{n}$是随着n增大而变化的。
接下来我们看一个例子:
这是一个看起来可能趋近于1的数列$\{x_{n}\}$,通项公式是
我们画出了前几项的散点图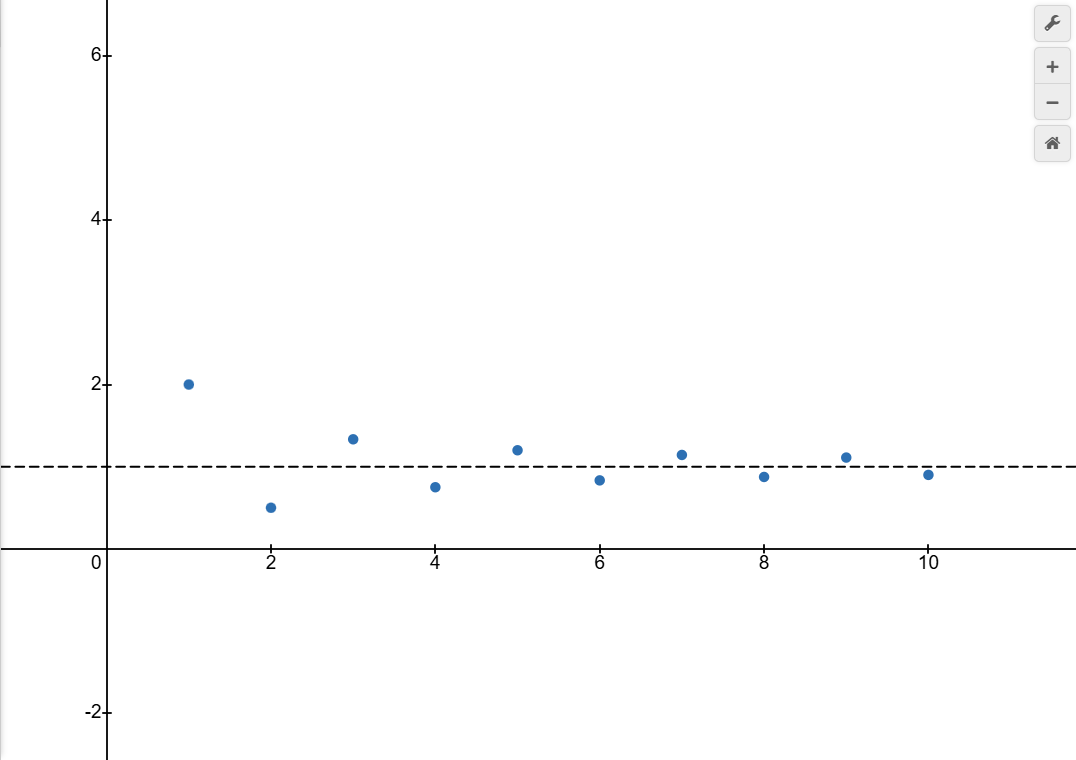
为了验证它是否真的趋近于1,我们在一定的精度下验证他,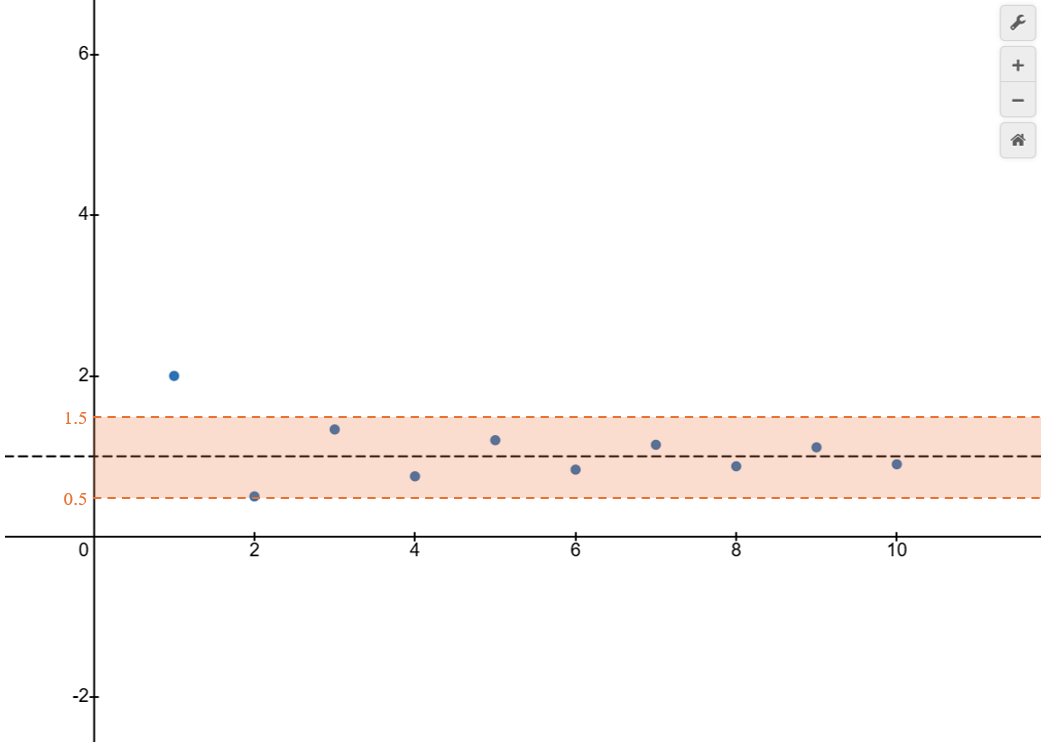
当我们取$1\pm 0.5$时,我们只要往后取几项,取到$n>2$就可以做到在精度内与1十分接近(也就是$x_{n}$与$1$的距离小于精度)
当然你可能说这也太粗糙了,不过没事我们可以继续提高精度。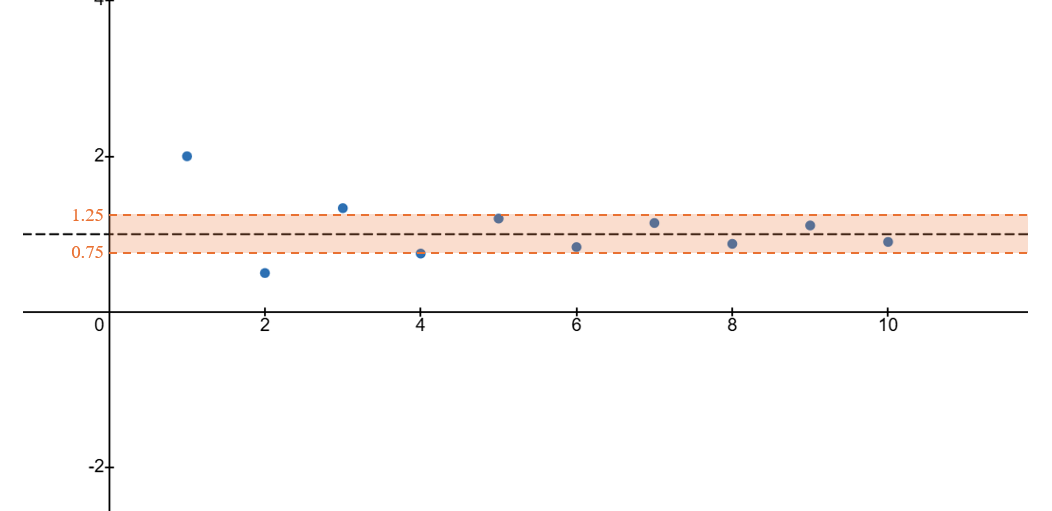
现在我们把精度提升到$1\pm 0.25$,这是我们依旧只要往后取几项,取到$n>4$就可以做到在精度内与1十分接近。
看起来我们就算一直缩小精度,只要把项数取得更多一点,也同样可以达到在精度内与1十分接近。
我们可以用式子算一算,只要能做到:“不管精度多小,只要n取得够大就能使$x_{n}$在精度内与1十分接近,也就是$x_{n}$与$1$的距离小于精度。”那就可以证明数列$\{x_{n}\}$趋近于1。
$x_{n}$与$1$的距离是
假如我们把精度提到$\frac{1}{100}$,那么我们可以把n取到$\frac{1}{1000}$,这样距离就会比精度更小;
假如我们把精度提到$\frac{1}{1000}$,那么我们可以把n取到$\frac{1}{10000}$,这样距离就会比精度更小;
假如我们把精度提到$\frac{1}{10000}$,那么我们可以把n取到$\frac{1}{100000}$,这样距离就会比精度更小……
因为是递减的,所以永远可以满足“不管精度多小,只要n取得够大就能使$x_{n}$与$1$的距离小于精度。”
太好了,这样我们就证明了数列$\{x_{n}\}$趋近于1。
把刚刚的过程改装一下,我们就可以得到极限的定义:
我们将“精度”用$\varepsilon$表示,将刚刚趋近的极限值用$a$表示,“取到$n>$多少就可以做到在精度内与a十分接近”里面的“多少”用正整数$N$表示,那么就有:
不管精度$\varepsilon$多小,只要$n$取得够大,满足$n>N$时就能使$x_{n}$在精度内与$a$十分接近,也就是$x_{n}$与$a$的距离小于精度$\varepsilon$
现在我们再看这个定义:
定义:设$\{x_{n}\}$为一数列,如果存在任意常数$a$,对于任意给定的正数$\varepsilon$,不论它有多小,总存在正整数$N$,使得当$n>N$时,不等式
都成立,那么就称常数$a$是数列$\{x_{n}\}$的极限(或者叫数列$\{x_{n}\}$收敛于$a$)。
记为
极限的性质
极限大概知道是啥了,现在就来看看性质:(证明略,参照课本)
①(极限的唯一性)如果数列$\{x_{n}\}$收敛,那么它的极限唯一。
②(收敛数列的有界性)如果数列$\{x_{n}\}$收敛,那么数列$\{x_{n}\}$一定有界。
有界是指存在正数$M$,使得对于一切$x_{n}$都满足不等式
则称数列$\{x_{n}\}$是有界的;反之,若不存在称为无界的。
当数列$\{x_{n}\}$无界时,它一定发散;但是当数列$\{x_{n}\}$有界时,它不一定收敛。
比如$x_{n}=(-1)^{n}$的数列$\{x_{n}\}$就是有界但不收敛。
③(收敛数列的保号性)如果$\lim_{x \to \infty}=a$,且$a>0$(或$a<0$),那么存在正整数$N$,当$n>N$时,都有$x_{n}>0$(或$x_{n}<0$)
推论:如果数列$\{x_{n}\}$从某项起有$x_{n}>0$(或$x_{n}<0$),且$\lim_{x \to \infty}=a$,那么$a>0$(或$a<0$)。
④(收敛数列和其子数列间的关系)如果数列$\{x_{n}\}$收敛于$a$,那么它的任一子数列也收敛,且极限也是$a$
函数的极限
函数的极限也差不多,除了当$|n|$接近正无穷的极限值外,还有$n$接近于某个特定值的极限值。
1 趋于有限值时的函数极限
概念
在此之前我们先认识几个概念
因为找函数某点极限的过程实际上指的是根据这个点附近函数的变化,通过不断逼近(缩小精度)的方式,“猜”出该点应该是多少。但是实际上这点不一定是这个值,甚至这一点可能都不存在。
比如这个函数$f(x)$: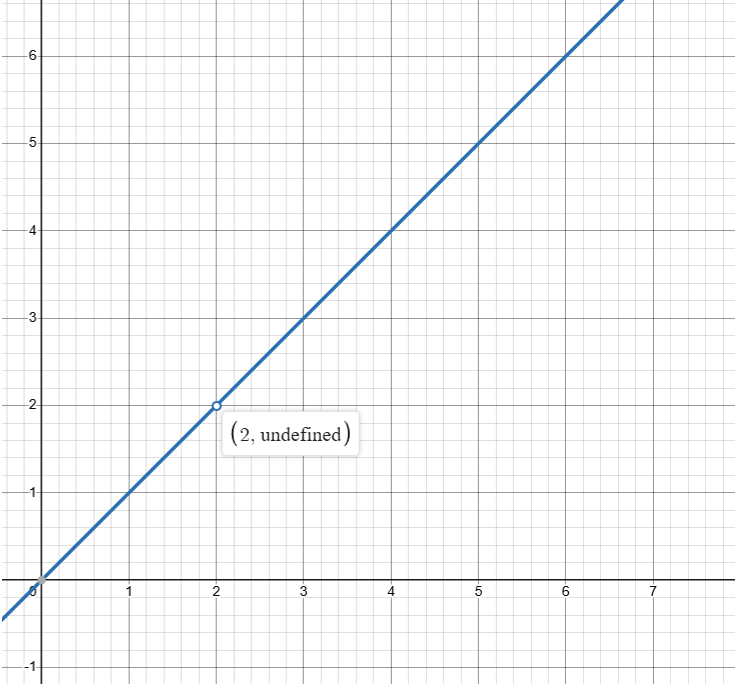
它在$x=2$处是没有定义的,但是我们依旧可以根据左右的变化,通过慢慢逼近这个点,“猜”出这里按理来说是2。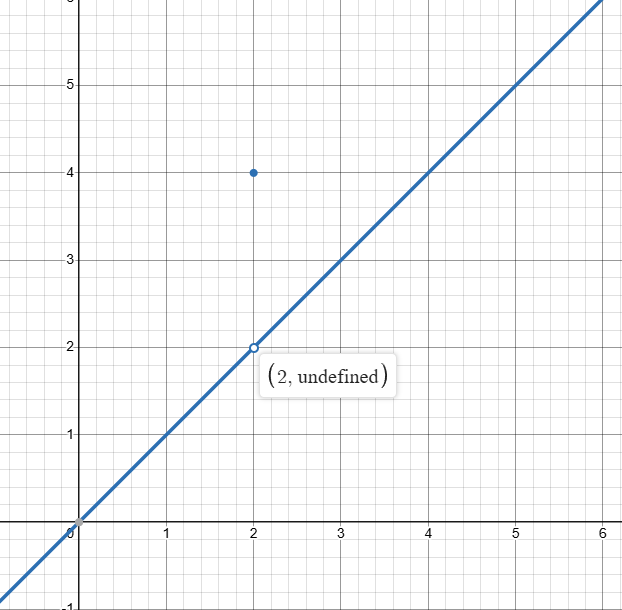
假如函数长这样,结果也是一样的,所以这一点的极限和这一点实际是多少没有任何关系。
为了防止我们求极限这个点$x=x_{0}$时出现取不到等等情况,我们通常把要逼近的这个点去掉,然后再进行取精度、不断逼近的操作。
我们把以$x_{0}$为中心的开区间称作点$x_{0}$的邻域,也就是以$x_{0}$为中心两端长为$\varepsilon$的范围。去掉中心$x_{0}$后的邻域称作点$x_{0}$的去心邻域。
邻域记作$U(x_{0})$,去心邻域记作$\overset{\circ}{U}(x_{0})$
刚刚我们还说到“逼近”,实际上我们可以从两边逼近,从左边逼近$x_{0}$称作左极限,从右边逼近$x_{0}$称作右极限,假如两侧逼近结果相同,就称为双侧极限存在,也就是我们说的该点存在极限。
我们用
表示左极限
用
表示右极限
双侧极限就用
表示。
定义
好了,现在我们就参照数列极限的定义给出函数极限的定义:
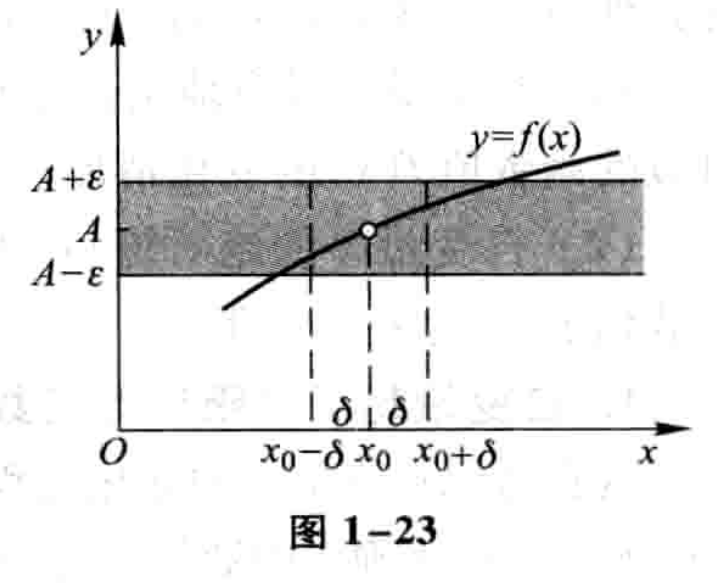
定义:设函数$f(x)$在某点$x_{0}$的某一去心邻域内有定义。如果存在常数$A$,对于任意给定的正数$\varepsilon$,不论它多小,总存在正数$\delta$,使得当$x$满足不等式$0<|x-x_{0}|<\delta$时,对应的函数值$f(x)$都满足不等式
那么常数$A$就称作函数$f(x)$当$x\rightarrow x_{0}$时的极限,记作
2 趋于无限大时的函数极限
定义:设函数$f(x)$当$|x|$大于某一正数时有定义。如果存在常数$A$,对于任意给定的正数$\varepsilon$,不论它多小,总存在正数$\delta$,使得当$x$满足不等式$|x|>X$时,对应的函数值$f(x)$都满足不等式
那么常数$A$就称作函数$f(x)$当$x\rightarrow \infty$时的极限,记作
此时,直线$y=A$是函数$f(x)$的图形的水平渐近线。