电荷与递推数列

物理作业上看到了这么一道题，详细研究后发现其中居然还蕴含了一个数学问题，于是就有了这篇文章。

题目

【题目】
1.有三个完全相同的金属球，球A带的电荷量为q，球B和球C均不带电。现把球A、B、C以各种接触顺序经若干次接触后分开，最后球B的电荷量不可能是（  ）
A. $\frac{3q}{8}$    B. $\frac{5q}{16}$    C. $\frac{q}{3}$    D. $\frac{9q}{32}$

【解析】
完全相同的金属球，接触后电荷平分，所以若先将A与B接触后分开，则A、B均带电量$\frac{q}{2}$，再将B与C接触，则B与C均带电量为$\frac{q}{4}$，再将A与B接触，则A与B带电量均为$\frac{1}{2}(\frac{q}{2}+\frac{q}{4})=\frac{3}{8}q$，再将B与C接触，则B与C带电量均为$\frac{1}{2}(\frac{3q}{8}+\frac{q}{4})=\frac{5}{16}q$，再将A与B接触，则A与B带电量均为$\frac{1}{2}(\frac{3q}{8}+\frac{5q}{16})=\frac{11}{32}q$，以此类推，最终三个带电体的电量均为$\frac{q}{3}$，故ABC均有可能，D不可能，故D正确，ABC错误。

【答案】D

解决

我想要求出所有可能答案的递推数列，为此我们先构建一个模型。

两个球相碰之后会平分电荷，之后为了继续改变电荷，只能和剩下一个球相碰。我们可以把这个过程看成这样：

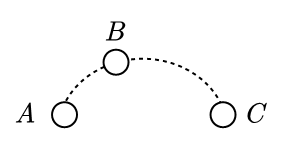
B球反复与A、C两球相碰，B球所有可能的电荷量就是该题答案。
现在我们将其抽象为数学问题：
可以看出，A、C就像一个储存器，储存着上两次的结果，而B每次就在A、C内写入平均值。
那么我们就能写出这个问题的数学形式：

$$数列\{a_{n}\}满足a_{1}=0，a_{2}=\frac{1}{2}，且当n\ge 3时，a_{n}满足a_{n}=\frac{1}{2}(a_{n-2}+a_{n-1})，试求该数列的通项公式。$$

接下来我们就解答这个数学问题。

用待定系数法构造一个只含n和n-1项的数列$\{b_{n}\}$，设

$$a_{n}+Xa_{n-1}=Y(a_{n-1}+Xa_{n-2})$$

解得

$$\left\{\begin{matrix} X=\frac{1}{2} \\ Y=1 \end{matrix}\right.$$

即为

$$a_{n}+\frac{1}{2}a_{n-1}=a_{n-1}+\frac{1}{2}a_{n-2}$$

所以设$b_{n}=a_{n}+\frac{1}{2}a_{n-1}$，得到

$$b_{3}=a_{3}+\frac{1}{2}a_{2}=\frac{1}{2}$$

由刚刚构造的式子又有

$$b_{n}=b_{n-1}=\frac{1}{2}$$

那么

$$a_{n}+\frac{1}{2}a_{n-1}=\frac{1}{2}$$

有了这个式子，我们可以裂项相消求解了

$$a_{n}+\frac{1}{2}a_{n-1}=\frac{1}{2}$$ $$-\frac{1}{2}a_{n-1}-\frac{1}{4}a_{n-2}=\frac{1}{2}\cdot (-\frac{1}{2})$$ $$\frac{1}{4}a_{n-2}+\frac{1}{8}a_{n-3}=\frac{1}{2}\cdot (-\frac{1}{2})^{2}$$ $$-\frac{1}{8}a_{n-3}-\frac{1}{16}a_{n-4}=\frac{1}{2}\cdot (-\frac{1}{2})^{3}$$ $$......$$ $$(-\frac{1}{2})^{n-3}a_{3}-(-\frac{1}{2})^{n-2}a_{2}=\frac{1}{2}\cdot (-\frac{1}{2})^{n-3}$$

全部相加得

$$a_{n}-(-\frac{1}{2})^{n-2}a_{2}=\frac{1}{2}(1+(-\frac{1}{2})+...+(-\frac{1}{2})^{n-3})$$

等比数列求和得

$$a_{n}-(-\frac{1}{2})^{n-2}a_{2}=\frac{1}{2}(\frac{2}{3}(1-(-\frac{1}{2})^{n-2}))$$

带入$a_{2}$最终化简得

$$\mathbf{a_{n}=\frac{1}{6}(-\frac{1}{2})^{n-2}+\frac{1}{3}}$$

这就是最终答案

用这个式子我们可以判断出AB可能出现而D不可能，对于C我们可以对这个数列取极限，显然有

$$\lim_{n \to \infty} a_{n}=\frac{1}{3}$$

所以C选项可以成立

结尾

其实就是想对它求极限才想到求通项公式，不过有人会说把三个球同时碰在一起不就行了吗，我认为不是。
假设三个球碰在一起后A球先分开，此时BC可以看作一个整体，接下来再把BC分开平分电荷，那么A、B、C电荷量就分别是$\frac{q}{2}$、$\frac{q}{4}$、$\frac{q}{4}$了。
能做到三个球同时碰在一起或分开吗？这个平分电荷的现象根本的原理是什么？这还有待我继续学习研究。。。